2022. 10. 1. 12:33ㆍ중등 수학/중2 수학(2학기)
사다리꼴과 등변사다리꼴의 정의
사다리꼴은 한 쌍의 대변이 평행한 사각형을 말합니다.

사다리꼴 중에서도 특별히 아랫변의 양 끝 각의 크기가 같은 사다리꼴을 등변사다리꼴이라고 해요.
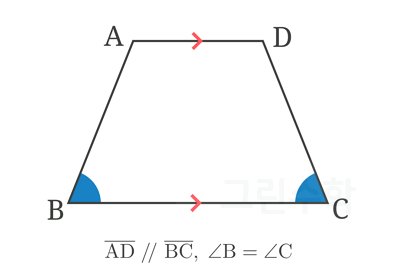
등변사다리꼴의 성질
(1) 평행하지 않은 두 대변의 길이가 같다.
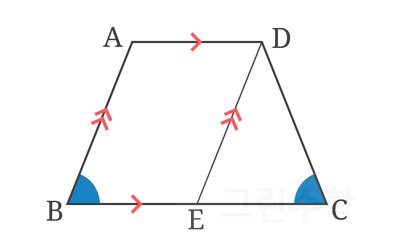
점 D를 지나면서 $\overline{\rm AB}$와 평행한 직선을 그리고, $\overline{\rm BC}$와 만나는 점을 E라고 할게요.
$\square{\rm ABCD}$는 평행사변형이므로
$\overline{\rm AB} = \overline{\rm DE}$ ······ ㉠
$\overline{\rm AB} \mparallel \overline{\rm DE}$ 이므로 $\angle{\rm B} = \angle{\rm DEC}$ (동위각)
그런데 $\angle{\rm B} = \angle{\rm C}$ 이므로 $\angle{\rm B} = \angle{\rm C} = \angle{\rm DEC}$
$\triangle{\rm DEC}$ 는 두 밑각의 크기가 같으므로 이등변삼각형입니다.
따라서, $\overline{\rm DE} = \overline{\rm DC}$ ······ ㉡
㉠, ㉡에 의해 $\overline{\rm AB} = \overline{\rm DE} = \overline{\rm DC}$
즉, 등변사다리꼴에서 평행하지 않은 두 대변의 길이는 같습니다.
(2) 두 대각선의 길이가 같다.

$\triangle{\rm ABC}$, $\triangle{\rm DCB}$에서
$\overline{\rm AB} = \overline{\rm DC}$ (등변사다리꼴의 성질)
$\angle{\rm B} = \angle{\rm C}$ (등변사다리꼴의 정의)
$\overline{\rm BC}$는 공통
따라서 $\triangle{\rm ABC} \equiv \triangle{\rm DCB}$ (SAS 합동)
대응변의 길이가 같으므로 $\overline{\rm AC} = \overline{\rm DB}$
즉, 등변사다리꼴의 두 대각선의 길이는 같습니다.
<등변사다리꼴의 성질 정리>

- 평행하지 않은 두 대변의 길이가 같다. ($\overline{\rm AB} = \overline{\rm DC}$)
- 두 대각선의 길이가 같다 ($\overline{\rm AC} = \overline{\rm DB}$)
'중등 수학 > 중2 수학(2학기)' 카테고리의 다른 글
| 평행선과 삼각형의 넓이, 높이가 같은 삼각형의 넓이의 비 (0) | 2022.10.22 |
|---|---|
| 여러 가지 사각형 사이의 관계 (0) | 2022.10.04 |
| 정사각형의 성질 (0) | 2022.01.08 |
| 마름모의 성질 (0) | 2021.12.29 |
| 직사각형의 성질 (0) | 2021.12.23 |