2021. 9. 28. 00:27ㆍ중등 수학/중2 수학(2학기)
삼각형의 외심의 위치
외심은 삼각형의 모양에 따라 위치가 달라져요.

예각삼각형의 외심: 삼각형의 내부
직각삼각형의 외심: 빗변의 중점
둔각삼각형의 외심: 삼각형의 외부
특히 직각삼각형의 외심이 빗변의 중점이라는 것이 아주 중요해요. 직각삼각형에서 외심은 빗변의 중점이므로 외접원의 반지름의 길이는 빗변의 길이의 절반이에요.
삼각형의 외심의 응용 - $ \angle x + \angle y + \angle z = 90^\circ $

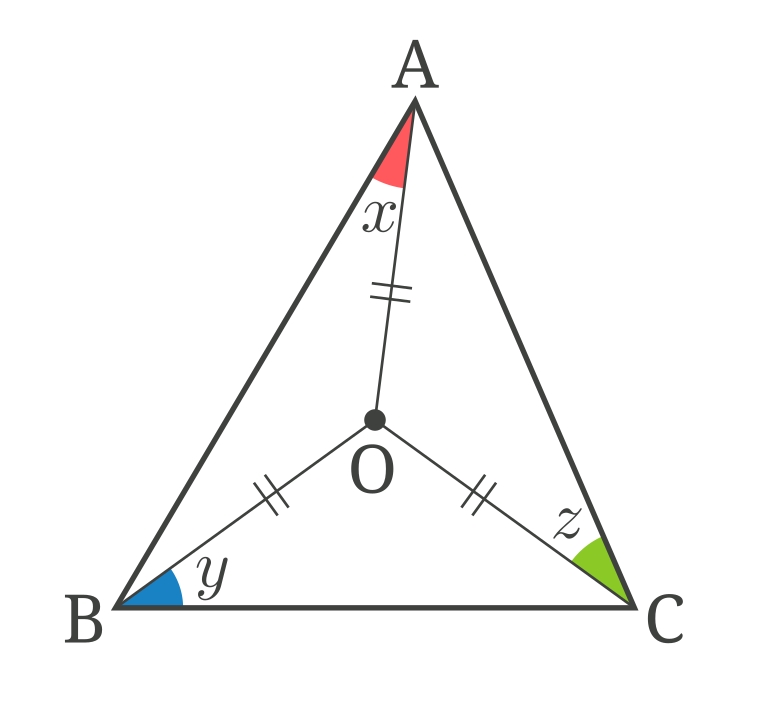
점 O는 $ \triangle{\rm ABC} $의 외심이에요.
외심에서 삼각형 세 꼭짓점까지의 거리는 모두 같죠?
$ \overline{\rm OA} = \overline{\rm OB} = \overline{\rm OC} $이니까 $ \triangle{\rm OAB} $, $ \triangle{\rm OBC} $, $ \triangle{\rm OCA} $는 모두 이등변삼각형이에요.
이등변삼각형 두 밑각의 크기는 같으니까
$ \angle{\rm OAB} = \angle{\rm OBA} = \angle x $
$ \angle{\rm OBC} = \angle{\rm OCB} = \angle y $
$ \angle{\rm OCA} = \angle{\rm OAC} = \angle z $
로 나타낼 수 있어요.
그러면 $ \triangle{\rm ABC} $에서
$ 2\angle x + 2\angle y + 2\angle z = 180^\circ $ 이므로
$ \angle x + \angle y + \angle z = 90^\circ $가 됩니다.
삼각형의 외심의 응용 - $ \angle{\rm BOC} = 2\angle{\rm A} $
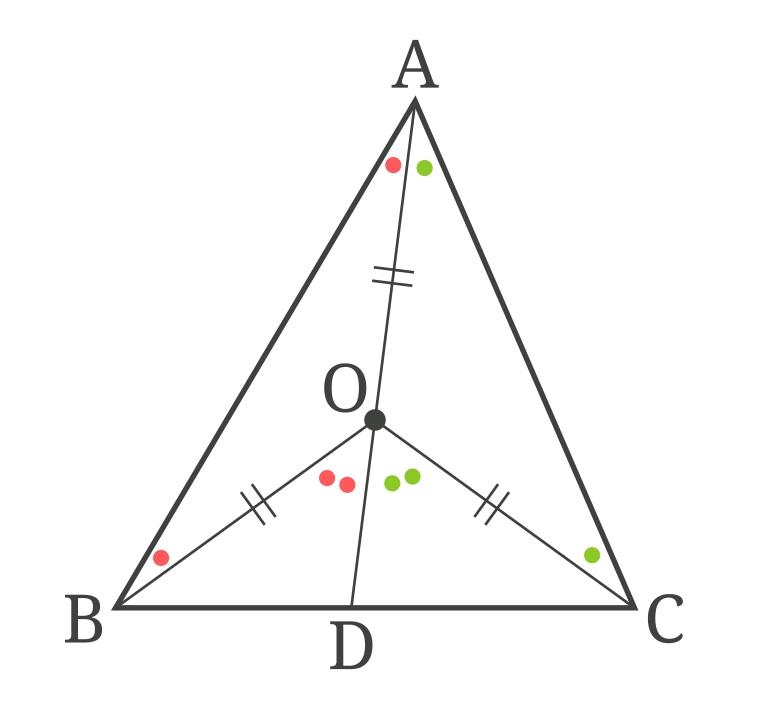
$ \overline{\rm AO} $의 연장선과 $ \overline{\rm BC} $의 교점을 D라고 할게요.
삼각형의 한 외각의 크기는 그와 이웃하지 않는 두 내각의 크기의 합과 같아요.
$ \angle{\rm BOD} = \angle{\rm OAB} + \angle{\rm OBA} = 2\angle{\rm OAB} $
$ \angle{\rm COD} = \angle{\rm OAC} + \angle{\rm OCA} = 2\angle{\rm OAC} $
따라서,
$ \angle{\rm BOC} = \angle{\rm BOD} + \angle{\rm COD} $
$ \angle{\rm BOC} $ $ = 2(\angle{\rm OAB} + \angle{\rm OAC}) $
$ \angle{\rm BOC} $ $ = 2 \angle{\rm A} $

'중등 수학 > 중2 수학(2학기)' 카테고리의 다른 글
| 삼각형의 내심(2) - 삼각형 내심의 응용 (0) | 2021.10.08 |
|---|---|
| 삼각형의 내심(1) - 삼각형 내심의 정의와 성질 (3) | 2021.10.04 |
| 삼각형의 외심(1) - 삼각형 외심의 정의와 성질 (3) | 2021.09.22 |
| 각의 이등분선의 성질 (0) | 2021.09.20 |
| 직각삼각형의 합동 조건 (2) | 2021.09.16 |