2021. 9. 16. 11:40ㆍ중등 수학/중2 수학(2학기)
삼각형의 합동 조건에는 3가지 경우가 있습니다.
SSS, SAS, ASA 합동이 있죠.
직각삼각형은 한 각이 직각인 삼각형입니다.
직각은 아주 특별한 각이에요.
삼각형의 세 내각의 합은 180º 이니까 딱 그 절반이죠?
그래서 직각이 아닌 나머지 두 각의 합도 90º가 돼요.
직각삼각형도 삼각형의 합동 조건에 맞아야 합동이라고 할 수 있어요.
그런데 직각이라는 아주 특별한 각을 갖고 있기 때문에 '삼각형의 합동 조건'이라는 까다로운 조건을 모두 보지 않아도 합동인지 아닌지를 빠르게 알 수가 있어요.
두 삼각형이 직각삼각형이고 빗변의 길이가 같으면, 한 예각의 크기 또는 한 변의 길이만 같아도 '합동이다'라고 할 수 있는 거죠!
직각삼각형의 합동 조건 - RHA 합동
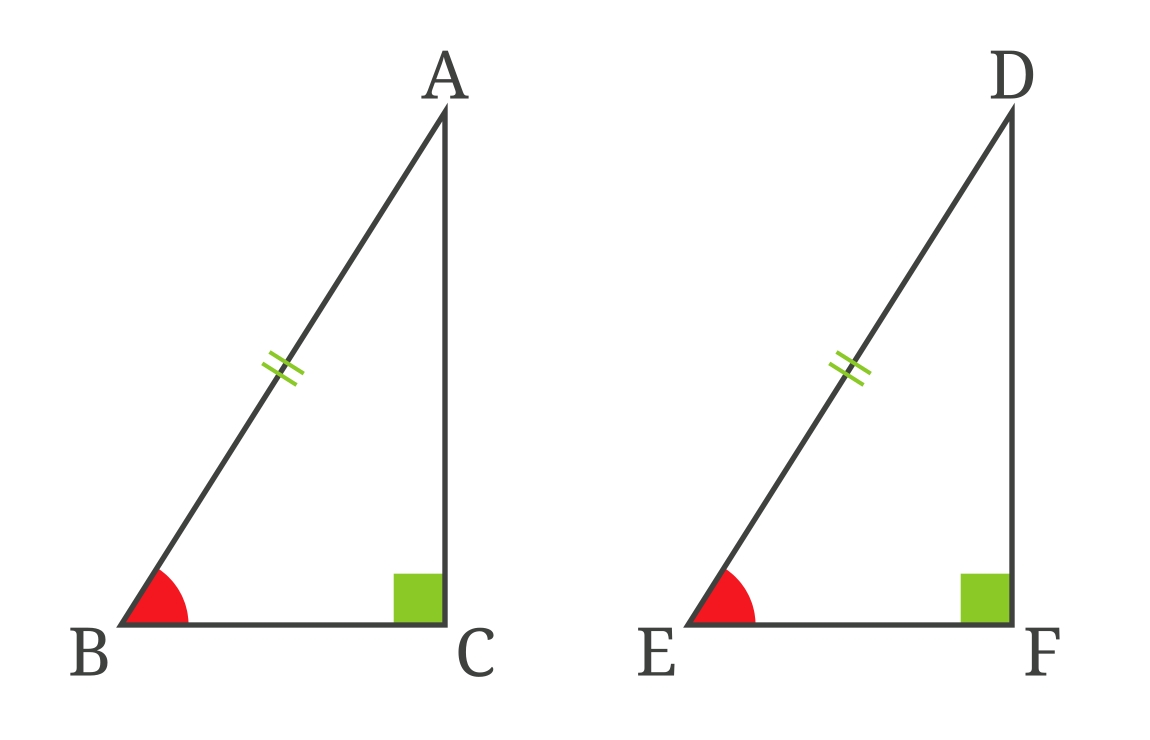
조건: $ \angle{\rm C} = \angle{\rm F} = 90^\circ $, $ \overline{\rm AB} = \overline{\rm DE}$ , $ \angle{\rm B} = \angle{\rm E} $
앞에서 직각이 아닌 나머지 두 각의 합이 90º라고 했죠?
$ \angle{\rm A} = 90^\circ - \angle{\rm B} $
$ \angle{\rm D} = 90^\circ - \angle{\rm E} $
$ \angle{\rm B} = \angle{\rm E} $이므로 $ \angle{\rm A} = \angle{\rm D} $
두 삼각형은 빗변의 길이가 같고 빗변의 양끝각의 크기가 같으므로
$ \triangle{\rm ABC} \equiv \triangle{\rm DEF} $ (ASA 합동)
두 삼각형이 직각(Right Angle), 빗변(Hypotenuse)의 길이와 한 예각(Angle)의 크기가 서로 같을 때 ASA 합동이 되는 것이 RHA 합동이에요.
직각삼각형의 합동 조건 - RHS 합동

두 삼각형이 직각(Right Angle), 빗변(Hypotenuse)의 길이와 다른 한 변(Side)의 길이가 서로 같을 때 합동이 되는 것을 RHS 합동이라고 해요.
RHS 합동은 RHA 합동을 이용해서 증명할 수 있어요.
조건: $ \angle{\rm C} = \angle{\rm F} = 90^\circ $, $ \overline{\rm AB} = \overline{\rm DE}$ , $ \overline{\rm AC} = \overline{\rm DF}$

$ \triangle{\rm DEF} $를 뒤집어 길이가 같은 두 변 AC와 DF가 겹치도록 놓아줍니다.
그러면 $ \triangle{\rm ABE} $가 새로 만들어지죠?
그런데 $ \overline{\rm AB} = \overline{\rm DE}$이니까 $ \triangle{\rm ABE} $는 이등변삼각형이에요.
이등변삼각형의 두 밑각의 크기는 같으니까(이등변삼각형의 성질) $ \angle{\rm B} = \angle{\rm E} $예요.
그러면 두 직각삼각형은 빗변의 길이와 한 예각의 크기가 서로 같으니까
$ \triangle{\rm ABC} \equiv \triangle{\rm DEF} $ (RHA 합동)
'중등 수학 > 중2 수학(2학기)' 카테고리의 다른 글
| 삼각형의 내심(1) - 삼각형 내심의 정의와 성질 (3) | 2021.10.04 |
|---|---|
| 삼각형의 외심(2) - 삼각형 외심의 응용 (2) | 2021.09.28 |
| 삼각형의 외심(1) - 삼각형 외심의 정의와 성질 (3) | 2021.09.22 |
| 각의 이등분선의 성질 (0) | 2021.09.20 |
| 이등변삼각형의 성질 (0) | 2021.09.12 |